Introduction to PROM validation

KB Christensen

Data analysis crash course

  • today: intro (data set, notation, ..), consistency, reliability (Cronbachs \(\alpha\)), invariance (DIF), local dependence, criterion validity
  • also today: CFA
  • after today: video lectures (examples in SAS and R), exercises on Absalon, ask question by e-mail to kach@sund.ku.dk
  • next time: Q & A, work on the exam together

Intro

  • data set (Exercise Adherence Rating Scale; EARS)
  • path diagrams

Exercise Adherence Rating Scale (EARS)

measuring adherence to prescribed home exercise

FILENAME preg URL "http://publicifsv.sund.ku.dk/~kach/scaleval/EARS.csv";
PROC IMPORT FILE=preg OUT=SASUSER.EARS DBMS=csv REPLACE;
GETNAMES=YES;
DELIMITER=';';
RUN;

https://www.sciencedirect.com/science/article/pii/S0031940616304801

Exercise Adherence Rating Scale (EARS)

measuring adherence to prescribed home exercise

EARS <- read.csv(url("http://publicifsv.sund.ku.dk/~kach/scaleval/EARS.csv"), sep=';')

https://www.sciencedirect.com/science/article/pii/S0031940616304801

Notation

Association between the variables \(A\) and \(B\) - and we believe that \(A\) causes \(B\). We put boxes around observed (manifest) variables

Notation

We put circles around unobserved (latent) variables. Will use \(\Theta\) or \(\theta\) (greek letter “theta”) to indicate latent variables.

Exercise Adherence Rating Scale (EARS)

Latent (unobservable) variable \(\Theta\), items \((X_i)_{i\in I}\), categorical exogenous variables \(Y\) (gender, age group)

SAS macro %itemmarg.sas()

FILENAME im URL 'https://raw.githubusercontent.com/KarlBangChristensen/itemmarg/master/itemmarg.sas';
%include im;
%ITEMMARG(DATA=SASUSER.EARS, ITEMS=item1-item6);

SAS macro %itemmarg.sas()

Bar chart of item score 0 1 2 3 4 PERCENT 0 10 20 30 40 50 60 70 80 90 100 item item item1 item2 item3 item4 item5 item6 item1 item2 item3 item4 item5 item6

BARplot R function

Install package (only do this once)

devtools::install_github("ERRTG/RASCHplot", build_vignettes = TRUE)

load package and plot

library(RASCHplot)
itemsIncomp <- EARS[,1:6]
BARplot(itemsIncomp, na.action = "na.rm")

BARplot R function

Consistency

  • items positively correlated because they all measure \(\theta\)

  • positive association with sum score (proxy for \(\theta\))

    many different correlations exist

Polychoric correlation

Metsämuuronen, Front. Appl. Math. Stat., Sec. Statistics and Probability, Volume 8 - 2022 https://doi.org/10.3389/fams.2022.914932, Figure 1.

Inter-item correlations, SAS

PROC CORR DATA=SASUSER.EARS POLYCHORIC NOPROB;
    VAR item1 item2;
    ODS SELECT PolychoricCorr;
RUN;
Polychoric Correlations
Variable With Variable N Correlation Wald Test LR Test
Standard
Error 		Chi-Square Pr > ChiSq Chi-Square Pr > ChiSq
item1 item2 192 0.44618 0.08031 30.8664 <.0001 23.0330 <.0001

Inter-item correlations, R

library(polycor)
polychor(EARS$item1, EARS$item2, std.err = TRUE, ML = TRUE)

Polychoric Correlation, ML est. = 0.4464 (0.0812)
Test of bivariate normality: Chisquare = 43.66, df = 15, p = 0.0001241

  Row Thresholds
  Threshold Std.Err.
1    -2.128  0.23080
2    -1.999  0.20420
3    -1.337  0.12550
4    -0.460  0.09386


  Column Thresholds
  Threshold Std.Err.
1   -0.9340  0.10560
2   -0.3552  0.09233
3    0.3530  0.09256
4    0.3668  0.09275

Inter-item correlations

Theoretical model

what we observe

Inter-item correlations, SAS

filename PMH URL "https://raw.githubusercontent.com/KarlBangChristensen/PolyHeatMap/master/PolyHeatMap.sas";
%include PMH;
%PolyHeatMap(dat=SASUSER.EARS, var=item1-item6);

Inter-item correlations, SAS

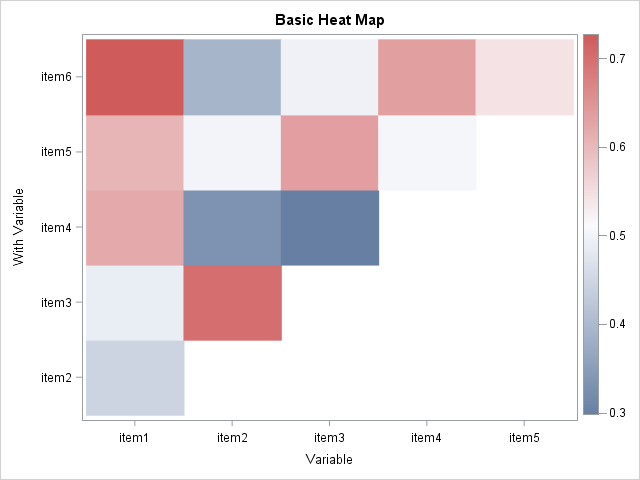
Inter-item correlations, R

cormat <- round(cor(items, use = "complete.obs"),2)
library(reshape2)
melted_cormat <- melt(cormat)
library(ggplot2)
ggplot(data = melted_cormat, aes(x=Var1, y=Var2, fill=value)) + 
  geom_tile()

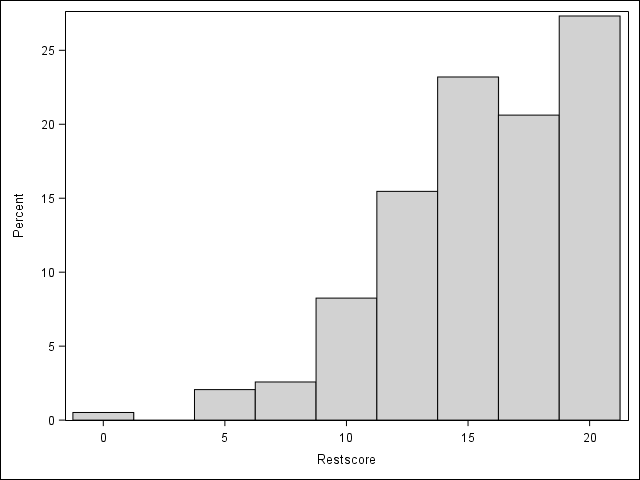
Total score

DATA WORK.EARS;
    SET SASUSER.EARS;
    score=SUM(OF item1-item6);
RUN; 
PROC SGPLOT DATA=WORK.EARS;
    HISTOGRAM score;
    DENSITY score / TYPE=KERNEL;
RUN;
The SGPlot Procedure 0 10 20 30 score 0 5 10 15 20 Percent Kernel

Add item-total correlations, SAS

FILENAME st URL 'https://raw.githubusercontent.com/KarlBangChristensen/scaletest/master/scaletest.sas';
%INCLUDE st;
data WORK.new(where=(nm=0));
    set SASUSER.EARS;
    nm=nmiss(of item1-item6);
run;
%scaletest(data=WORK.new, ncat=5, items=item1-item6, type=SPEARMAN);

Add item-total correlations, SAS

name mean SD _min _max floor ceiling Item total
item1 3.55 0.78 0.36 0.61 1.6 67.4 item1 0.65
item2 2.17 1.51 0.26 0.60 17.5 35.1 item2 0.76
item3 1.96 1.51 0.22 0.60 21.5 29.2 item3 0.79
item4 3.60 0.76 0.22 0.50 1.0 72.8 item4 0.53
item5 3.20 1.36 0.36 0.46 9.8 70.6 item5 0.72
item6 3.49 0.93 0.32 0.61 3.6 . item6 0.66

Add item-total correlations, R

library(devtools)
gh <- "https://raw.githubusercontent.com/KarlBangChristensen/scaletest/master/scaletest.R"
source_url(gh)
scaletest(data = items, min_item_score = 0, max_item_score = 4)
          mean        sd     floor  ceiling       min       max item_score_corr
item1 3.549223 0.7765522  1.554404 67.35751 0.3015623 0.4983621       0.6502836
item2 2.170103 1.5088454 17.525773 35.05155 0.2316051 0.5982678       0.7306689
item3 1.958974 1.5054400 21.538462 29.23077 0.2075063 0.5982678       0.7791156
item4 3.600000 0.7557341  1.025641 72.82051 0.2075063 0.4315206       0.5486745
item5 3.195876 1.3553897  9.793814 70.61856 0.3371068 0.4623874       0.7403411
item6 3.487179 0.9325664  3.589744 68.71795 0.2316051 0.4983621       0.6199170
       raw_corr
item1 0.5393439
item2 0.5240605
item3 0.5987229
item4 0.4252349
item5 0.5650794
item6 0.4784750

Visualizing item-total correlation

ods graphics on;
ods html5 style=htmlblue;
options nonotes;
DATA WORK.EARS;
    SET SASUSER.EARS;
    score=SUM(OF item1-item6);
RUN; 
PROC RANK data=WORK.EARS out=WORK.grouped groups=5;
    VAR score;
    RANKS scoregroup;
RUN;
PROC MEANS DATA=WORK.grouped;
    VAR item1;
    CLASS scoregroup;
    OUTPUT OUT=item1means MEAN=m LCLM=l UCLM=u;
RUN;
PROC SGPLOT DATA=WORK.item1means;
    BAND X=scoregroup LOWER=l UPPER=u / LEGENDLABEL='95% CI';
    SERIES X=scoregroup Y=m;
    LABEL m='Mean score on anxiety item';
RUN;
Analysis Variable : item1
Rank for Variable score N Obs N Mean Std Dev Minimum Maximum
0 38 36 2.8333333 1.1084094 0 4.0000000
1 41 41 3.1951220 0.7489831 1.0000000 4.0000000
2 29 29 3.6551724 0.4837253 3.0000000 4.0000000
3 46 46 3.9565217 0.2948839 2.0000000 4.0000000
4 41 41 4.0000000 0 4.0000000 4.0000000
The SGPlot Procedure 0 1 2 3 4 Rank for Variable score 2.5 3.0 3.5 4.0 Mean score on anxiety item Mean score on anxiety item 95% CI

Reliability

\(\alpha\) is a measure of

  • consistency: inter-item correlations positive ?
  • reliability: how precisely does the score measure \(\theta\) ?

compute \(\alpha\), SAS

PROC CORR DATA=SASUSER.EARS ALPHA NOMISS;
    VAR item1-item6;
    ODS SELECT "Cronbach Coefficient Alpha";
RUN;

\(\alpha\), SAS

Cronbach Coefficient Alpha
Variables Alpha
Raw 0.755560
Standardized 0.774217

compute \(\alpha\), R

only do this once

install.packages("multilevel", repos="http://cran.rstudio.com/")

compute \(\alpha\)

library(multilevel)
cr <- cronbach(items)
cr$Alpha
[1] 0.75556

\(\alpha\)

is a lower boundary of the reliability

\(\alpha\)

is a lower boundary of the reliability, but only if items are unidimensional and there is no local dependence.

\(\alpha\)

is a lower boundary of the reliability, but only if items are unidimensional and there is no local dependence. It is not a measure of validity.

Invariance (no differential item functioning; DIF)

Notation

\[ X_i\perp Y|\Theta \]

the item response does not depend directly on a covariate \(Y\)

Covariate

the covariate long groups respondents in two groups.

  • an association between long and an item should only occur because of an association between long and the latent variable.

Correlation ..

.. measures the degree of association between two random variables \(X\) and \(Y\)

Partial correlation

.. measures the degree of association between \(X\) and \(Y\), with the of a controlling variable \(Y\) removed

\[ \hat{\rho}_{XY\cdot\mathbf{Z}}=\frac{N\sum_{i=1}^N r_{X,i}r_{Y,i}-\sum_{i=1}^N r_{X,i}\sum_{i=1}^N r_{Y,i}} {\sqrt{N\sum_{i=1}^N r_{X,i}^2-\left(\sum_{i=1}^N r_{X,i}\right)^2}~\sqrt{N\sum_{i=1}^N r_{Y,i}^2-\left(\sum_{i=1}^N r_{Y,i}\right)^2}} \]

Can be used to explain (some of) the correlation between \(X\) and \(Y\). We can test if \(Z\) explains all of the correlation between \(X\) and \(Y\)

Correlation and partial correlation

DATA WORK.EARS;
    SET SASUSER.EARS;
    score=SUM(OF item1-item6);
RUN; 
PROC CORR DATA=WORK.EARS SPEARMAN NOSIMPLE FISHER;
    VAR item2;
    WITH long;
RUN;

Correlation and partial correlation

DATA WORK.EARS;
    SET SASUSER.EARS;
    score=SUM(OF item1-item6);
RUN; 
PROC CORR DATA=WORK.EARS SPEARMAN NOSIMPLE FISHER;
    VAR item2;
    WITH long;
    PARTIAL score;
RUN;

Correlation

Spearman Correlation Statistics (Fisher's z Transformation)
Variable With Variable N Sample Correlation Fisher's z Bias Adjustment Correlation Estimate 95% Confidence Limits p Value for
H0:Rho=0
item2 long 162 -0.19229 -0.19472 -0.0005972 -0.19172 -0.335979 -0.038663 0.0141

this is not evidence that something is wrong with the item

Partial correlation

Spearman Partial Correlation Statistics (Fisher's z Transformation)
Variable With Variable N N Partialled Sample Correlation Fisher's z Bias Adjustment Correlation Estimate 95% Confidence Limits p Value for
H0: Partial Rho=0
item2 long 162 1 -0.17629 -0.17815 -0.0005509 -0.17575 -0.321684 -0.021668 0.0251

members of the two groups with the same total score differ significantly so there is a problem with the item.

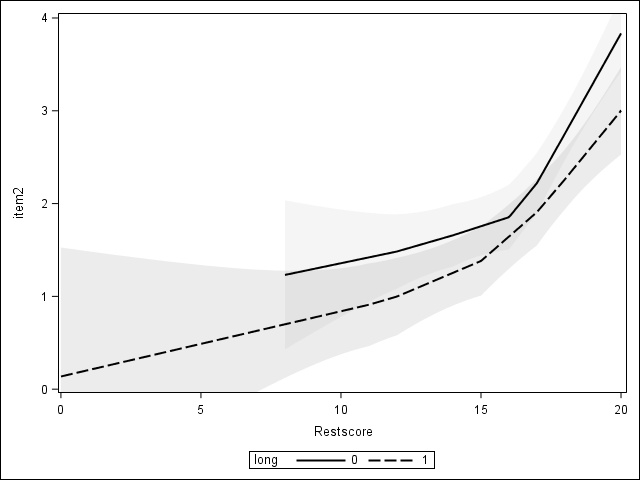
DIF can be visualized

* INCLUDE MACRO;


* USE MACRO;

DIF can be visualized

* INCLUDE MACRO;
FILENAME difp URL 'http://192.38.117.59/~kach/macro/difplot.sas';
%INCLUDE difp;
* USE MACRO;

DIF can be visualized

* INCLUDE MACRO;
FILENAME difp URL 'http://192.38.117.59/~kach/macro/difplot.sas';
%INCLUDE difp;
* USE MACRO;
%difplot(DATA=SASUSER.EARS, 
         DIFITEM=item2, 
         ITEMS=item1-item6, 
         EXO=long, 
         OUTFILE=difplot, 
         YMAX=4);

DIF can be visualized

The SGPlot Procedure



The SGPlot Procedure


Looking for DIF

Test DIF using

  • Mantel-Haenszel
  • Partial correlation
  • Logistic regression

Local dependence

Four testable assumption - three ((i), (ii), and (iii)) are intuitive. However (iv) local independence is a technical assumption and it is not as intuitive.

(iv) local independence

trick

think of \(X_4\) as an exogenous variable and handle this as a DIF problem.

  • score is \(R_4=X_1+X_2+X_3\)
  • we test conditional independence \(X_3\perp X_4|R_4\)

trick

a similar argument where \(X_3\) and \(X_4\) switch places

  • compute (rest) score \(R_3=X_1+X_2+X_4\)
  • test \(X_3\perp X_4|R_3\)

Tjur (1982). Scandinavian Journal of Statistics, 9, 23–30. http://www.jstor.org/stable/4615850

SAS macro

FILENAME TJUR URL 'http://192.38.117.59/~kach/macro/tjur.sas';
%INCLUDE TJUR;
DATA WORK.nm;
  SET SASUSER.EARS;
  IF NMISS(OF item1-item6)>0 THEN DELETE;
RUN;
%TJUR(DATA=WORK.nm, ITEMS=item1-item6);
PROC PRINT DATA=TJUR NOOBS;
  WHERE _TYPE_='CORR';
  VAR _name_ item1-item6;
  FORMAT item1-item6 8.2;
RUN;

Local dependence in EARS data

15 item pairs (two partial correlations for each of them).

name item1 item2 item3 item4 item5 item6
item1 1.00 -0.12 -0.15 0.20 0.15 0.31
item2 -0.22 1.00 0.29 -0.11 -0.11 -0.23
item3 -0.21 0.35 1.00 -0.25 0.05 -0.09
item4 0.17 -0.09 -0.27 1.00 0.02 0.24
item5 0.09 -0.09 0.01 0.02 1.00 -0.05
item6 0.27 -0.21 -0.11 0.24 -0.05 1.00

let’s focus

item1 item2 item3 item4 item5 item6
item1 1.00
item2 1.00 0.29
item3 0.35 1.00
item4 1.00
item5 1.00
item6 0.01

Using R

Read data and calculate rest scores

EARS <- read.csv(url("http://publicifsv.sund.ku.dk/~kach/scaleval/EARS.csv"), sep=';')
items <- EARS[,c("item1","item2","item3","item4","item5","item6")]
nm <- items[complete.cases(items),]
nm$rscore1 <-            nm$item2 + nm$item3 + nm$item4 + nm$item5 + nm$item6
nm$rscore2 <- nm$item1 +            nm$item3 + nm$item4 + nm$item5 + nm$item6
nm$rscore3 <- nm$item1 + nm$item2 +            nm$item4 + nm$item5 + nm$item6

Using R

calculate (some of) the partial correlations

library(ppcor)
round(pcor.test(x=nm$item2, y=nm$item3, z=nm$rscore2)$estimate, digits = 2)
round(pcor.test(x=nm$item2, y=nm$item3, z=nm$rscore3)$estimate, digits = 2)
[1] 0.35
[1] 0.29

Criterion validity

  • latent variable \(\Theta\)
  • score = item1 + … + item6 indirect measure of \(\Theta\)
  • for any variable \(Z\) where \[\textrm{corr}(Z,\Theta)>0\] we expect \(\textrm{corr}(Z,\)score\()>0\)
  • This can be tested

Confirmatory factor analysis (CFA) ..

.. is essentially a statistical model that incorporates all the assumptions we have discussed.

  • Testing the fit of a CFA model to your data will tell you if the instrument is valid

Two types of factor analysis

  • Exploratory factor analysis (EFA): Data is explored to determine the number of underlying factors. Prior knowledge about data generating mechanisms is ignored. Will not be considered here.

  • Confirmatory factor analysis (CFA): Based on prior knowledge a factor structure is postulated and tested against data.

Methods originally developed for continuous items and an assumption of multivariate normal distribution.

CFA model for EARS data

Statistical model for the joint distribution of all items and covariates

CFA model

Statistical model for the joint distribution of all items and covariates

  • Allows inclusion of DIF and local dependence
  • (Allows models with a multivariate latent variable)
  • Builds on the normal distribution

CFA model

CFA model for one factor

  • Data on \(p\) items for subject \(i\)
  • vector \(\boldsymbol{x}_i=(x_{i1},...,x_{ip})^t\).
  • underlying variable \(\theta_i\).
  • Model \[ \begin{array}{lcl} x_{i1}& = &\nu_1+\lambda_1 \theta_i + \epsilon_{i1}\\ &:\\ x_{ip} &= &\nu_p+\lambda_p \theta_i + \epsilon_{ip} \end{array} \]
  • Latent variable and measurement errors follow normal distribution
  • \(\theta_i \sim N(\alpha,\psi)\) independent of \(\epsilon_{ij} \sim N(0, \omega_j)\)

Parameters

  • \(\lambda_j:\) factor loading,
  • \(\omega_j:\) measurement error variance

CFA model in matrix form

\[ \boldsymbol{x}_i=\nu + \boldsymbol{\Lambda} \boldsymbol{\theta}_i + \boldsymbol{\epsilon}_i \] vectors \(\boldsymbol{\theta}_i\) and \(\boldsymbol{\epsilon}_i\) are independent,

\[ \boldsymbol{\theta}_i \sim N(\boldsymbol{\alpha},\boldsymbol{\Psi})\;\;\;\; \boldsymbol{\epsilon}_i\sim N(0,\boldsymbol{\Omega}) \] - \(\Omega\) diagonal matrix. - Error uncorrelated.

local indpendence

  • \(\Omega\) is typically a diagonal matrix.
  • Error terms are assumed to be uncorrelated.
  • This is the assumption of local independence
  • Latent variable is the only reason the items are correlated.

Path diagrams

  • Boxes: observed variables
  • Circles or ovals: latent variables
  • One headed arrows: linear effects
  • Two headed arrows: un-directional associations

Dimensionality

we only consider uni-dimensional CFA models, but CFA also works for multi-dimensional models.

  • if the CFA model fits the data we conclude that there is no evidence against the null hypothesis the the instrument is uni-dimensional

  • items are assumed to be continuous and error terms normally distributed

  • We are not very happy about the normality assumption

Model

\[ \begin{array}{lcl} x_{i1}& = &\nu_1+\lambda_1 \theta_i + \epsilon_{i1}\\ &:\\ x_{ip} &= &\nu_p+\lambda_p \theta_i + \epsilon_{ip} \end{array} \]

  • \(\lambda_j:\) factor loading,
  • \(V(\epsilon_{ip})=\omega_j:\) measurement error variance
  • local dependence = correlated error terms
  • local independence = uncorrelated error terms

Path diagram EARS data

  • Boxes: observed variables
  • Circles or ovals: latent variables
  • One headed arrows: linear effects
  • Two headed arrows: un-directional associations

local independence

Measurement errors \((\epsilon_1,\ldots,\epsilon_6)\) independent \[ \Omega= \begin{bmatrix} \sigma_1^2&0&0&0&0&0\\ 0&\sigma_2^2&0&0&0&0\\ 0&0&\sigma_3^2&0&0&0\\ 0&0&0&\sigma_4^2&0&0\\ 0&0&0&0&\sigma_5^2&0\\ 0&0&0&0&0&\sigma_6^2 \end{bmatrix} \]

Estimation

For identification we fix \(V(\Theta)=1\) this means that \[ \textrm{corr}(X_j,\Theta)=\lambda_j\;\;\;V(\epsilon_{j})=1-\lambda_j^2 \]

High \(\lambda\)-value \(\rightarrow\) item is precise.

  • no test for item quality only assessed indirectly by inspecting the \(\lambda\)’s

CFA model induces structure in correlation

\[ \textrm{corr}_{\lambda}(X)= \left( \begin{array}{ccccc} 1 \\ \lambda_2\lambda_1 & 1 \\ \lambda_3\lambda_1 & \lambda_3\lambda_2 & 1& \\ \vdots&\vdots&\ddots&\ddots\\ \lambda_6\lambda_1 & \lambda_6\lambda_2 & \cdots & \lambda_6\lambda_5 & 1\\ \end{array}\right) \]

Estimate CFA model using PROC CALIS in SAS

PROC CALIS DATA=SASUSER.EARS;
LINEQS
    item1 = lam1 * F + E1,
    item2 = lam2 * F + E2,
    item3 = lam3 * F + E3,
    item4 = lam4 * F + E4,
    item5 = lam5 * F + E5,
    item6 = lam6 * F + E6;
    STD
    F = 1;
    ODS SELECT Calis.StandardizedResults.LINEQSEqStd;
RUN;

Output PROC CALIS in SAS

Covariance Structure Analysis: Maximum Likelihood Estimation

Standardized Results for Linear Equations
item1 =   0.6582 (**) F + 1.0000   E1
item2 =   0.5952 (**) F + 1.0000   E2
item3 =   0.6578 (**) F + 1.0000   E3
item4 =   0.4931 (**) F + 1.0000   E4
item5 =   0.6430 (**) F + 1.0000   E5
item6 =   0.5733 (**) F + 1.0000   E6

Estimate CFA model using lavaan in R

library(lavaan)
EARS <- read.csv(url("http://publicifsv.sund.ku.dk/~kach/scaleval/EARS.csv"), sep=';')
EARS.model.1 <- 'Theta =~ item1+item2+item3+item4+item5+item6'
fit <- cfa(EARS.model.1, data=EARS, likelihood='wishart')
standardizedsolution(fit)

Output lavaan in R

     lhs op   rhs est.std    se      z pvalue ci.lower ci.upper
1  Theta =~ item1   0.658 0.054 12.161      0    0.552    0.764
2  Theta =~ item2   0.595 0.059 10.147      0    0.480    0.710
3  Theta =~ item3   0.658 0.054 12.150      0    0.552    0.764
4  Theta =~ item4   0.493 0.066  7.511      0    0.364    0.622
5  Theta =~ item5   0.643 0.055 11.647      0    0.535    0.751
6  Theta =~ item6   0.573 0.060  9.519      0    0.455    0.691
7  item1 ~~ item1   0.567 0.071  7.956      0    0.427    0.706
8  item2 ~~ item2   0.646 0.070  9.247      0    0.509    0.783
9  item3 ~~ item3   0.567 0.071  7.962      0    0.428    0.707
10 item4 ~~ item4   0.757 0.065 11.693      0    0.630    0.884
11 item5 ~~ item5   0.587 0.071  8.260      0    0.447    0.726
12 item6 ~~ item6   0.671 0.069  9.724      0    0.536    0.807
13 Theta ~~ Theta   1.000 0.000     NA     NA    1.000    1.000

Chi-squared test of model fit

The fit of the model is tested by comparing

  • \(\left( \begin{array}{ccccc} 1 \\ \lambda_2\lambda_1 & 1 \\ \lambda_3\lambda_1 & \lambda_3\lambda_2 & 1& \\ \vdots&\vdots&\ddots&\ddots\\ \lambda_6\lambda_1 & \lambda_6\lambda_2 & \cdots & \lambda_6\lambda_5 & 1\\ \end{array}\right)\)

and

  • \(\left( \begin{array}{cccc} 1 \\ \rho_{21} & 1 \\ \vdots & \ddots & \ddots \\ \rho_{51} & \cdots & \rho_{54} & 1 &\\ \rho_{61} & \cdots & \rho_{64} & \rho_{65} & 1\\ \end{array}\right)\)

Degrees of freedom

The unrestricted model has 21 parameters (6 variances and 15 correlations) and in the CFA model we are testing there are 12 parameters (6 \(\lambda\)’s and 6 \(\epsilon\)’s).

  • Degrees of freedom: \(df=21-12=9\)

SAS

ods html5 style=htmlblue;
PROC CALIS DATA=SASUSER.EARS;
LINEQS
    item1 = lam1 * F + E1,
    item2 = lam2 * F + E2,
    item3 = lam3 * F + E3,
    item4 = lam4 * F + E4,
    item5 = lam5 * F + E5,
    item6 = lam6 * F + E6;
    STD
    F = 1;
    FITINDEX NOINDEXTYPE ON(ONLY)=[NOBS CHISQ DF PROBCHI];
    ODS SELECT "Fit Summary";
RUN;

Covariance Structure Analysis: Maximum Likelihood Estimation

Fit Summary
Number of Observations 191
Chi-Square 59.0301
Chi-Square DF 9
Pr > Chi-Square <.0001

R

library(lavaan)
EARS <- read.csv(url("http://publicifsv.sund.ku.dk/~kach/scaleval/EARS.csv"), sep=';')
EARS.model.1 <- 'Theta =~ item1+item2+item3+item4+item5+item6'
fit <- cfa(EARS.model.1, data=EARS, likelihood='wishart')
fitMeasures(fit, c("ntotal","chisq","df","p-value"))
ntotal  chisq     df 
191.00  59.03   9.00

Test logic is backward

Lower power increases the chance that you will retain the model.

The Root Mean Square Error Of Approximation (RMSEA)

  • \(\mbox{RMSEA}=\sqrt{\frac{\chi^2-df}{df (N-1)}}\).
  • If model is correct then \(\chi^2 \approx df\) and RMSEA is close to 0.
  • If model is wrong \(\chi^2 > df\) and RMSEA is high.
  • RMSEA is a measure of badness-of-fit

Root Mean Square Error Of Approximation

  • There is no \(p\)-value in RMSEA.
  • It is not clear what levels to expect if the model is correct.
  • Often used cut-off value: RMSEA \(\leq 0.05\)

Model fit evaluation

  • Both \(\chi^2\) and RMSEA measure over-all fit.
  • Some parts of the model may be very wrong, even in models that pass the test.
  • Test logic is backward: Lower power increases the chance that you will retain the model.
  • Upper CI for RMSEA does not have this problem.

SAS

Covariance Structure Analysis: Maximum Likelihood Estimation

Fit Summary
Number of Observations 191
Chi-Square 59.0301
Chi-Square DF 9
Pr > Chi-Square <.0001
RMSEA Estimate 0.1710
RMSEA Lower 90% Confidence Limit 0.1311
RMSEA Upper 90% Confidence Limit 0.2138

R

        ntotal          chisq             df          rmsea rmsea.ci.lower 
       191.000         59.030          9.000          0.171          0.131 
rmsea.ci.upper 
         0.214

So in the EARS data set the test against the unrestricted model rejects the hypothesis:

  • \(\chi^2\)=59.0, df= 12, p<0.0001.
  • \(RMSEA\)=0.171 (95% CI 0.131 to 0.214)

Modification indices ..

.. measure how much better model-fit would become if a fixed parameter was set free to be estimated.

  • If a parameter \(\beta\) fixed, e.g. \(\beta=0\), MI tests the hypothesis \(H_0:\beta=0\) against the alternative \(H_a:\beta\ne0\).
  • under \(H_0\) the distribution of \(MI\) is \(\chi^2_1\)
  • if \(MI\) is high the corresponding model restriction is not supported by the data.

Relax assumption in model

\[ \begin{bmatrix} x_{i1}\\ \vdots\\ x_{i6} \end{bmatrix} = \begin{bmatrix} \lambda_{1}\\ \vdots\\ \lambda_{6}\\ \end{bmatrix} \cdot \theta_i + \begin{bmatrix} \epsilon_{i1}\\ \vdots\\ \epsilon_{i6}\\ \end{bmatrix} \]

by allowing correlation between error terms between \(\epsilon_k\) and \(\epsilon_l\):

\[ cov(\epsilon_k, \epsilon_l) \ne 0 \] For example

\[ \Omega= \begin{bmatrix} \sigma_1^2&0&0&0&0&0\\ 0&\sigma_2^2&0&0&\boldsymbol{\rho}&0\\ 0&0&\sigma_3^2&0&0&0\\ 0&0&0&\sigma_4^2&0&0\\ 0&\boldsymbol{\rho}&0&0&\sigma_5^2&0\\ 0&0&0&0&0&\sigma_6^2\\ \end{bmatrix} \]

  • for fixed value of latent variable the items \(y_k\) and \(y_l\) are correlated.
  • There are 15 different item pairs and we can add the pair with the highest MI (we prefer only to do this if makes subject matter sense).

Let’s compute and print (some of the) MI’s using R

library(lavaan)
EARS <- read.csv(url("http://publicifsv.sund.ku.dk/~kach/scaleval/EARS.csv"), sep=';')
EARS.model.1 <- 
  'Theta =~ item1+item2+item3+item4+item5+item6'
fit <- cfa(EARS.model.1, data=EARS, likelihood='wishart')
MI <- modificationindices(fit)
MI[c(1:10),]
     lhs op   rhs     mi    epc sepc.lv sepc.all sepc.nox
14 item1 ~~ item2  6.612 -0.178  -0.178   -0.250   -0.250
15 item1 ~~ item3 10.013 -0.222  -0.222   -0.333   -0.333
16 item1 ~~ item4  4.092  0.069   0.069    0.182    0.182
17 item1 ~~ item5  0.638  0.049   0.049    0.082    0.082
18 item1 ~~ item6 13.047  0.153   0.153    0.343    0.343
19 item2 ~~ item3 39.954  0.848   0.848    0.614    0.614
20 item2 ~~ item4  1.236 -0.074  -0.074   -0.095   -0.095
21 item2 ~~ item5  0.186 -0.051  -0.051   -0.041   -0.041
22 item2 ~~ item6  8.255 -0.237  -0.237   -0.256   -0.256
23 item3 ~~ item4 10.912 -0.218  -0.218   -0.296   -0.296

Adding a parameter using SAS

ods html5 style=htmlblue;
PROC CALIS DATA=SASUSER.EARS;
LINEQS
    item1 = lam1 * F + E1,
    item2 = lam2 * F + E2,
    item3 = lam3 * F + E3,
    item4 = lam4 * F + E4,
    item5 = lam5 * F + E5,
    item6 = lam6 * F + E6;
    STD
    F = 1;
    COV E2 E3=rho;
    FITINDEX NOINDEXTYPE ON(ONLY)=[NOBS CHISQ DF PROBCHI RMSEA RMSEA_LL RMSEA_UL];
    ODS SELECT "Fit Summary";
RUN;

Covariance Structure Analysis: Maximum Likelihood Estimation

Fit Summary
Number of Observations 191
Chi-Square 20.8272
Chi-Square DF 8
Pr > Chi-Square 0.0076
RMSEA Estimate 0.0919
RMSEA Lower 90% Confidence Limit 0.0442
RMSEA Upper 90% Confidence Limit 0.1412

add correlated error terms

\[ \Omega= \begin{bmatrix} \sigma_1^2&0&0&0&0&0\\ 0&\sigma_2^2&\boldsymbol{\rho}&0&0&0\\ 0&\boldsymbol{\rho}&\sigma_3^2&0&0&0\\ 0&0&0&\sigma_4^2&0&0\\ 0&0&0&0&\sigma_5^2&0\\ 0&0&0&0&0&\sigma_6^2\\ \end{bmatrix} \]

Adding a parameter using R

library(lavaan)
EARS <- read.csv(url("http://publicifsv.sund.ku.dk/~kach/scaleval/EARS.csv"), sep=';')
EARS.model.2 <- 
  'Theta =~ item1+item2+item3+item4+item5+item6
  item2 ~~ item3'
fit <- cfa(EARS.model.2, data=EARS, likelihood='wishart')
fitMeasures(fit, c("ntotal","chisq","df","p-value","rmsea","rmsea.ci.lower","rmsea.ci.upper"))
        ntotal          chisq             df          rmsea rmsea.ci.lower 
       191.000         20.827          8.000          0.092          0.044 
rmsea.ci.upper 
         0.141

Summary

  • Model fit is improved by adding correlated error term,
  • but still the fit is not not good.
  • Note \(df=8\) (before it was \(9\)).
  • We can add more correlated error terms

evaluating DIF using CFA ..

.. is done using multiple groups CFA (MG-CFA)

two groups in the EARS data

Frequency
Table of long by item1
long item1
. 0 1 2 3 4 Total
.
6
0
0
3
8
20
37
0
0
1
1
4
24
61
91
1
1
2
0
6
14
49
72
Total
7
3
1
13
46
130
200
Frequency
Table of long by item2
long item2
. 0 1 2 3 4 Total
.
5
5
8
7
0
12
37
0
1
13
14
23
1
39
91
1
0
16
14
25
0
17
72
Total
6
34
36
55
1
68
200
Frequency
Table of long by item3
long item3
. 0 1 2 3 4 Total
.
5
8
9
9
1
5
37
0
0
18
16
25
2
30
91
1
0
16
16
18
0
22
72
Total
5
42
41
52
3
57
200
Frequency
Table of long by item4
long item4
. 0 1 2 3 4 Total
.
5
0
1
4
6
21
37
0
0
1
0
5
18
67
91
1
0
1
0
8
9
54
72
Total
5
2
1
17
33
142
200
Frequency
Table of long by item5
long item5
. 0 1 2 3 4 Total
.
6
4
0
7
1
19
37
0
0
7
2
12
1
69
91
1
0
8
4
11
0
49
72
Total
6
19
6
30
2
137
200
Frequency
Table of long by item6
long item6
. 0 2 3 4 Total
.
5
2
5
9
16
37
0
0
2
4
19
66
91
1
0
3
9
8
52
72
Total
5
7
18
36
134
200

omit missing

ods html5 style=htmlblue;
DATA SASUSER.EARS_NM(WHERE=(nm=0));
  SET SASUSER.EARS;
  nm=NMISS(OF long item1-item6);
RUN;

two groups in the EARS data

Frequency
Table of long by item1
long item1
0 1 2 3 4 Total
0
1
1
4
24
60
90
1
2
0
6
14
49
71
Total
3
1
10
38
109
161
Frequency
Table of long by item2
long item2
0 1 2 3 4 Total
0
13
14
23
1
39
90
1
16
14
24
0
17
71
Total
29
28
47
1
56
161
Frequency
Table of long by item3
long item3
0 1 2 3 4 Total
0
18
16
25
2
29
90
1
16
15
18
0
22
71
Total
34
31
43
2
51
161
Frequency
Table of long by item4
long item4
0 2 3 4 Total
0
1
5
18
66
90
1
1
7
9
54
71
Total
2
12
27
120
161
Frequency
Table of long by item5
long item5
0 1 2 3 4 Total
0
7
2
12
1
68
90
1
7
4
11
0
49
71
Total
14
6
23
1
117
161
Frequency
Table of long by item6
long item6
0 2 3 4 Total
0
2
4
19
65
90
1
3
8
8
52
71
Total
5
12
27
117
161

CFA in one sub group

ods html5 style=htmlblue;
PROC CALIS DATA=SASUSER.EARS_NM PLOT=PATHDIAGRAM mod;
WHERE long=0;
LINEQS
    item1 = lam1 * F + E1,
    item2 = lam2 * F + E2,
    item3 = lam3 * F + E3,
    item4 = lam4 * F + E4,
    item5 = lam5 * F + E5,
    item6 = lam6 * F + E6;
    STD
    F = 1;
    PATHDIAGRAM DIAGRAM=[STANDARD] FITINDEX=[NOBS CHISQ DF PROBCHI]; 
    ODS SELECT 'Standardized';
RUN;

Covariance Structure Analysis: Maximum Likelihood Estimation

Path Diagram Standardized Solution 0.00 Pr > Chi-sq 9 DF 31.83 Chi-sq 90 N Obs

CFA in the other sub group

ods html5 style=htmlblue;
PROC CALIS DATA=SASUSER.EARS_NM PLOT=PATHDIAGRAM mod;
WHERE long=1;
LINEQS
    item1 = lam1 * F + E1,
    item2 = lam2 * F + E2,
    item3 = lam3 * F + E3,
    item4 = lam4 * F + E4,
    item5 = lam5 * F + E5,
    item6 = lam6 * F + E6;
    STD
    F = 1;
    PATHDIAGRAM DIAGRAM=[STANDARD] FITINDEX=[NOBS CHISQ DF PROBCHI]; 
    ODS SELECT 'Standardized';
RUN;

Covariance Structure Analysis: Maximum Likelihood Estimation

Path Diagram Standardized Solution 0.00 Pr > Chi-sq 9 DF 27.73 Chi-sq 71 N Obs

Let’s expand our simple CFA

let \(\boldsymbol{X}^{(1)}\) and \(\boldsymbol{X}^{(2)}\) denote data the two groups. configural invariance.

\[ \boldsymbol{X}^{(1)}=\boldsymbol{\nu}^{(1)}+\boldsymbol{\lambda}^{(1)}\cdot\theta+\boldsymbol{\epsilon}\;\;\;\;\boldsymbol{\epsilon}\sim N(0,\Omega^{(1)}) \] \[ \boldsymbol{X}^{(2)}=\boldsymbol{\nu}^{(2)}+\boldsymbol{\lambda}^{(2)}\cdot\theta+\boldsymbol{\epsilon}\;\;\;\;\boldsymbol{\epsilon}\sim N(0,\Omega^{(2)}) \]

Later we can impose one or more of the different restrictions \[ \boldsymbol{\nu}^{(1)}=\boldsymbol{\nu}^{(2)}\;\;\;\;\boldsymbol{\lambda}^{(1)}=\boldsymbol{\lambda}^{(2)}\;\;\;\;\Omega^{(1)}=\Omega^{(2)} \]

Configural invariance

ods html5 style=htmlblue;
PROC CALIS PLOT=PATHDIAGRAM mod;
    group 1 / data=SASUSER.EARS_nm(where=(long=1));
    group 2 / data=SASUSER.EARS_nm(where=(long=0));
    MODEL 1 / GROUP=1;
    LINEQS
    item1 = nu1_1*Intercept + lam1_1*F + E1,
    item2 = nu2_1*Intercept + lam2_1*F + E2,
    item3 = nu3_1*Intercept + lam3_1*F + E3,
    item4 = nu4_1*Intercept + lam4_1*F + E4,
    item5 = nu5_1*Intercept + lam5_1*F + E5,
    item6 = nu6_1*Intercept + lam6_1*F + E6;
    MEAN F=0;
    STD
    E1 = eps1_1,
    E2 = eps2_1,
    E3 = eps3_1,
    E4 = eps4_1,
    E5 = eps5_1,
    E6 = eps6_1,
    F=1;
    MODEL 2 / GROUP=2;
    LINEQS
    item1 = nu1_2*Intercept + lam1_2*F + E1,
    item2 = nu2_2*Intercept + lam2_2*F + E2,
    item3 = nu3_2*Intercept + lam3_2*F + E3,
    item4 = nu4_2*Intercept + lam4_2*F + E4,
    item5 = nu5_2*Intercept + lam5_2*F + E5,
    item6 = nu6_2*Intercept + lam6_2*F + E6;
    MEAN F=0;
    STD
    E1 = eps1_2,
    E2 = eps2_2,
    E3 = eps3_2,
    E4 = eps4_2,
    E5 = eps5_2,
    E6 = eps6_2,
    F=1;
    FITINDEX ON(ONLY) = [NOBS CHISQ DF PROBCHI]; 
    ODS SELECT "Fit Summary" ML.Model1.LINEQSEq ML.Model2.LINEQSEq; 
RUN;

Mean and Covariance Structures: Maximum Likelihood Estimation

Fit Summary
Modeling Info Number of Observations 161
Absolute Index Chi-Square 59.5643
  Chi-Square DF 18
  Pr > Chi-Square <.0001

Mean and Covariance Structures: Maximum Likelihood Estimation

Model 1. Linear Equations
item1 =   3.5211 (**) Intercept + 0.6313 (**) F + 1.0000   E1
item2 =   1.8310 (**) Intercept + 0.8764 (**) F + 1.0000   E2
item3 =   1.9577 (**) Intercept + 1.0125 (**) F + 1.0000   E3
item4 =   3.6197 (**) Intercept + 0.4819 (**) F + 1.0000   E4
item5 =   3.1268 (**) Intercept + 1.0309 (**) F + 1.0000   E5
item6 =   3.4930 (**) Intercept + 0.6510 (**) F + 1.0000   E6
Model 2. Linear Equations
item1 =   3.5667 (**) Intercept + 0.3907 (**) F + 1.0000   E1
item2 =   2.4333 (**) Intercept + 1.1762 (**) F + 1.0000   E2
item3 =   2.0889 (**) Intercept + 1.2299 (**) F + 1.0000   E3
item4 =   3.6444 (**) Intercept + 0.2105 (**) F + 1.0000   E4
item5 =   3.3444 (**) Intercept + 0.6100 (**) F + 1.0000   E5
item6 =   3.6111 (**) Intercept + 0.3292 (**) F + 1.0000   E6

Configural invariance

Mean and Covariance Structures: Maximum Likelihood Estimation

Fit Summary
Modeling Info Number of Observations 161
Absolute Index Chi-Square 59.5643
  Chi-Square DF 18
  Pr > Chi-Square <.0001

Mean and Covariance Structures: Maximum Likelihood Estimation

Model 1. Linear Equations
item1 =   3.5211 (**) Intercept + 0.6313 (**) F + 1.0000   E1
item2 =   1.8310 (**) Intercept + 0.8764 (**) F + 1.0000   E2
item3 =   1.9577 (**) Intercept + 1.0125 (**) F + 1.0000   E3
item4 =   3.6197 (**) Intercept + 0.4819 (**) F + 1.0000   E4
item5 =   3.1268 (**) Intercept + 1.0309 (**) F + 1.0000   E5
item6 =   3.4930 (**) Intercept + 0.6510 (**) F + 1.0000   E6
Model 2. Linear Equations
item1 =   3.5667 (**) Intercept + 0.3907 (**) F + 1.0000   E1
item2 =   2.4333 (**) Intercept + 1.1762 (**) F + 1.0000   E2
item3 =   2.0889 (**) Intercept + 1.2299 (**) F + 1.0000   E3
item4 =   3.6444 (**) Intercept + 0.2105 (**) F + 1.0000   E4
item5 =   3.3444 (**) Intercept + 0.6100 (**) F + 1.0000   E5
item6 =   3.6111 (**) Intercept + 0.3292 (**) F + 1.0000   E6

This makes sense

  • \(9+9=18\) degrees of freedom
  • \(\chi^2=31.83+27.72=59.6\)

Evidence of DIF from earlier

Spearman Partial Correlation Statistics (Fisher's z Transformation)
Variable With Variable N N Partialled Sample Correlation Fisher's z Bias Adjustment Correlation Estimate 95% Confidence Limits p Value for
H0: Partial Rho=0
item2 long 162 1 -0.17629 -0.17815 -0.0005509 -0.17575 -0.321684 -0.021668 0.0251

members of the two groups with the same total score differ significantly so there is a problem with the item.

Let’s include this - model with partial invariance

Mean and Covariance Structures: Maximum Likelihood Estimation

Model 1. Linear Equations
item1 =   3.5542 (**) Intercept + 0.6060 (**) F + 1.0000   E1
item2 =   1.8982 (**) Intercept + 0.9224 (**) F + 1.0000   E2
item3 =   2.0479 (**) Intercept + 1.2101 (**) F + 1.0000   E3
item4 =   3.6393 (**) Intercept + 0.4160 (**) F + 1.0000   E4
item5 =   3.2572 (**) Intercept + 1.0051 (**) F + 1.0000   E5
item6 =   3.5720 (**) Intercept + 0.5847 (**) F + 1.0000   E6
Model 2. Linear Equations
item1 =   3.5542 (**) Intercept + 0.6060 (**) F + 1.0000   E1
item2 =   2.3888 (**) Intercept + 1.3663 (**) F + 1.0000   E2
item3 =   2.0479 (**) Intercept + 1.2101 (**) F + 1.0000   E3
item4 =   3.6393 (**) Intercept + 0.4160 (**) F + 1.0000   E4
item5 =   3.2572 (**) Intercept + 1.0051 (**) F + 1.0000   E5
item6 =   3.5720 (**) Intercept + 0.5847 (**) F + 1.0000   E6

Let’s include this - model with partial invariance

Mean and Covariance Structures: Maximum Likelihood Estimation

Fit Summary
Modeling Info Number of Observations 161
Absolute Index Chi-Square 69.1437
  Chi-Square DF 27
  Pr > Chi-Square <.0001

Should be compared to this model (scalar invariance)

Mean and Covariance Structures: Maximum Likelihood Estimation

Fit Summary
Modeling Info Number of Observations 161
Absolute Index Chi-Square 75.4021
  Chi-Square DF 28
  Pr > Chi-Square <.0001